Technical Note 1
SciSoft Company (www.SciSoftCo.com)
Detrending of dual and single-sine data in jClamp -- detrending now exposed in jClamp
Cell membrane capacitance can be measured with the 2-sine or phase track technique in jClamp. Either a 2-sine or single sine stimulus can be superimposed on any waveform created in the Command Utility.
 Single Sine.
Single Sine.
 Dual Sine.
Dual Sine.
The response from a simple cell model is shown below.
 Dual Sine.
Dual Sine.
 Single Sine.
Single Sine.
The response from dual sine stimulation is analyzed with FFT to obtain the real and imaginary components at each stimulus frequency. These data are used to determine the parameters of a simple model of the recorded cell – a series resistance in series with a parallel combination of a membrane resistance and membrane capacitance. The equations are from Pusch and Neher, 1988. I outlined the application of their equations to the novel 2-sine technique in one of my grant proposals in 1992, which is photocopied in the appendix below, along with the final progress report of the grant. It makes for interesting reading!
Single sine stimulation can also be used to measure membrane capacitance with the same cell model.
See jClamp’s help file for details.
Each technique requires that you obtain a calibration file that is used to correct for the frequency response of the patch clamp system (electrode, amplifier, filters). Correcting for the system response is important since the parameter solutions are model dependent and assume that the system response is flat. It is the job of the calibration file to flatten the unflat system response. It is important for correct measurement that the electrode’s stray capacitance (which is not included in the model) is balanced out during pipette-membrane seal formation.
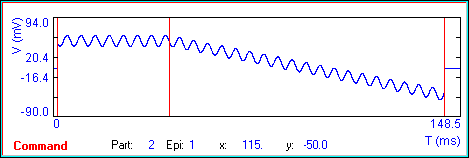
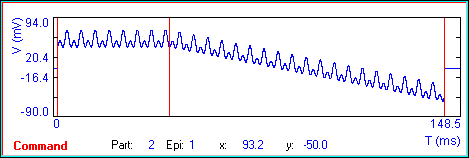
Another important step to take for proper parameter estimation is detrending of the data. FFT measures of selected frequencies (in our case the frequencies of the stimulating sine waves) are best evaluated if other slow time dependent changes in the response are removed. In jClamp, if you superimpose the stimulating sine waves on a time varying stimulus, e.g. a ramp or slow sine wave, then it is best to remove this slowly changing response from the data prior to FFTing. I use a linear approach to detrending, but it is on a very small (relative) time scale so it avoids problems with whole dataset nonlinearity.
An example: Given a 10us clock and a 128 ms ramp with 2 sine stimuli superimposed at a resolution of 1.28 ms (these are all set in the command utility), there are 100 repetitions of a unit stimulus consisting of one period of the low frequency (f1) component and 2 periods of the high frequency (f2) component (the ratio of f2 to f1 is 2). I detrend on the scale of the unit stimulus, which for the whole stimulus (100 times larger) proves to be much better than full linear detrending, and I think on par with a nonlinear (spline) approach. The success of this “piece-wise linear” approach is shown below.
Here I have used the math model in jClamp to generate nonlinear responses owing to a voltage dependent capacitance. A difference equation technique is used in the model to obtain solutions. The nonlinear capacitance derives from the first derivative (re: voltage) of a simple two-state Boltzmann charge transfer. Below I stimulate with ramps (with the two sine technique) of differing rates using jClamp’s incrementing time feature.
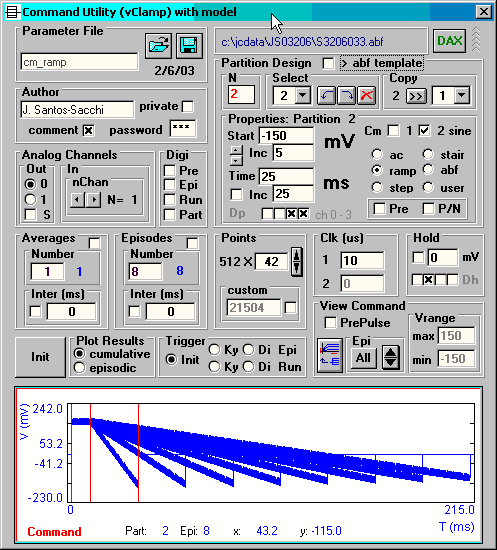
Below is the capacitance plot derived from the incrementing ramp stimulations.
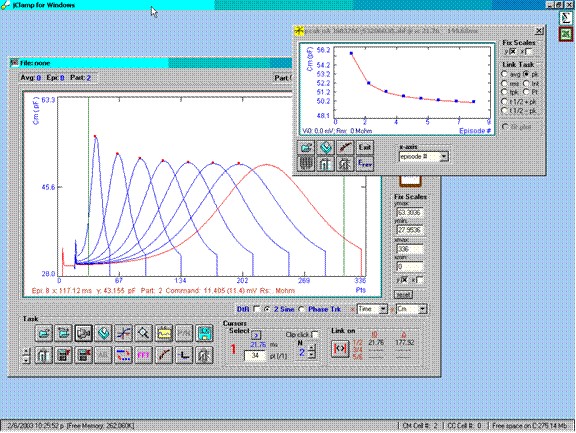
In the analysis window I plot all episodes. It is clear that the magnitude of the peaks of capacitance depend on ramp rate, the faster the ramp rate, the larger the peak, even though the model parameters are the same for each ramp data collection. The I-V plot window clearly shows the relationship.
Several years ago I implemented detrending in jClamp because of this potential problem. If you use only step stimuli then these is no rate problem (except at onset!). Below is the response when the detrending feature of jClamp is enabled.
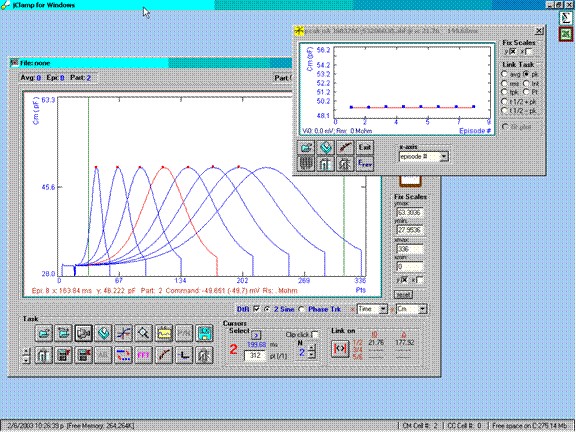
The response is in accord with the set model parameters. I should note that the generation of currents by the model is independent of the analysis procedure, so it is unlikely that the effect of ramp rate is due to model evaluation with the difference equation technique. Furthermore, the clock was sufficiently fast and the same for all ramps -- 10 us.
I have looked at real data and the effects of ramp speed are not so obvious as in model data, but to play it safe, I implemented detrending several years ago in jClamp. Recently, (jClamp V. 10.5) I have exposed detrending to the user, so that you may enable or disable it. It is probably a good approach for analysis of data obtained with stimuli of rapid rates, but I have found that it may introduce some noise into the measurements.
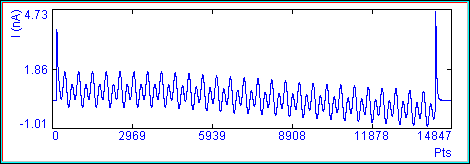
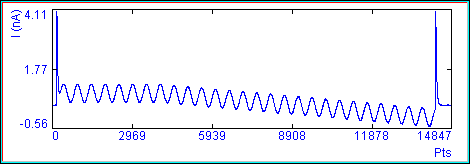
Below I have added noise to the current response prior to analysis. If detrend is used then the noise depends on the magnitude of the capacitance, however if detrend is off then the noise is small and uniform in the face of capacitance increase.
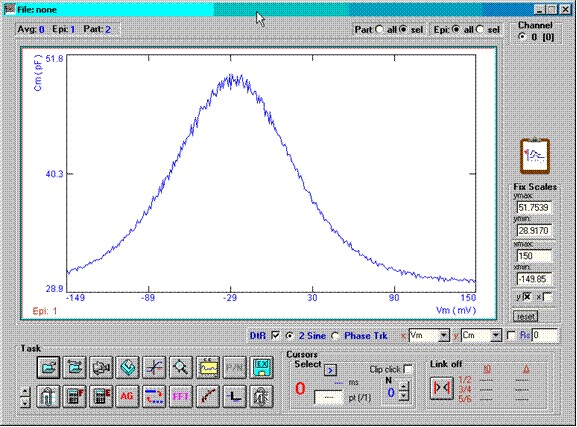
With detrending (DtR check box checked).
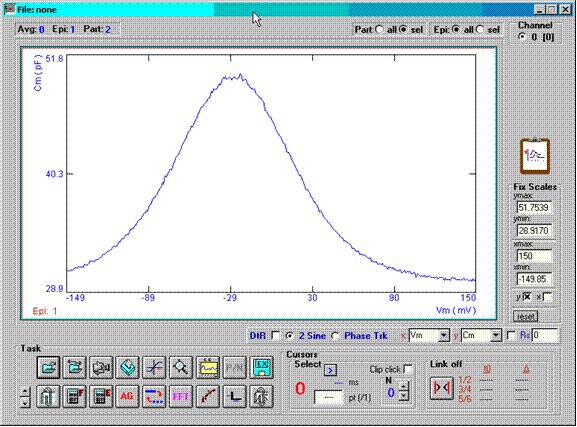
No detrending (DtR checkbox unchecked).
You can now decide whether to use detrending. If the underlying stimulus rate is fast and a small noise increase is not crucial then use detrending, else disable detrending.
